PRML-01.1, 예시: 다학식 곡선 피팅

Introduction

  • 간단한 회귀 문제로 예시로 든다.
  • ,
    • N=10으로 데이터 개수
    • x는 같은 거리를 가지는 x 축의 값이라고 생각
    • t는 sin(2*pi*x)+가우시안 noise이다.
    • 물론 실제 데이터는 가우시안 노이즈가 아닌 랜덤 노이즈기 때문에 실제 상황은 아니다.
  • 우리의 목표는 훈련 집합들을 사용한 모델을 가지고 새로운 입력값 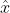을 가지고 타깃 변수 을 예측하는 것이다.
    • 이는 노이즈로 인해 관측 값(t)들이 변질되어 있기 때문에 쉽지 않은 문제이다.
  • 약식으로 진행을 하는데에 있어서 다음과 같은 다항식을 활용할 수 있다.
    • 즉 실제로는 sin그래프지만 다항식 그래프로 생각하여 식을 구성한 것이다.
    • M은 다항식의 차수이고 이는 선형 모델이라 불린다.
  • 훈련 집합의 표적값들의 값과 함숫값 y(x,w)의 오차 함수를 정의해 보자.
    • 이 함수는 L2 loss라고 일반적으로 부름
    • 1/2이 추가되는 것은 후반부에서 설명한다고 하는데 back-propgataion으로 모델을 학습할 때, 계산 상(수식 상)의 편의를 위해서임

연습 문제 1.1

  • 문제라기 보다는 w*(optimal)은 loss식이 최소하되는 w을 말하는 것이기 때문에 미분해서 나온 w에 대한 선형식을 풀면 된다는 것

  • 그렇다면 M은 어떻게 결정할까?
  • 다음 그림은 M=0, 1, 3, 9에 따라 피팅하는 예시이다.
  • 위 그림에서 M=0, 1일 때는 잘 표현하지 못하고 M=3이 가장 유사하다.
  • M=9에서는 훈련 집합에(파랑색) 대해서 완벽한 피팅이 가능하다.
  • 즉 loss=0이 되지만, 피팅 곡선이 심하게 진동하고 실제 함수인 sin(2*pi*x)를 표현하는데 적합하지 않다.
    • 이것을 과적합(over-fitting)이라고 부른다.
  • 이렇게 학습한 곡선으로 테스트를 해보자.
    • 테스트 데이터는 학습 데이터와 똑같이 만들되 노이즈만 다르게 적용하여 100개를 구성한다.
    • 시험 집합에 대한 오차는 다음과 같이 RMS(root mean square) error으로 확인한다.
      • N을 나눔으로써 데이터 사이즈에 의존성을 지운다.(평균 값 개념을 취한다는 것)
      • Root을 씌움으로써 E(w)의 정의인 제곱을 제거해준다.
    • M=0~9로 변경하면서 결과를 도출하였다.
      • M=9일때는 훈련데이터의 RMS 값이 0인데, 훈련 데이터 개수가 10개이므로 자유도가 10이상이면 무조건 피팅을 시킬 수 있기 때문이다.
      • 하지만 그만큼 진동이 심하게 된다.
    • 하지만 실제로 M=9인 것은 M=3인 곡선을 포함하는 관계이다.
      • 즉 M=9로 피팅시킨 곡선은 M=3으로 피팅시킨 곡선의 결과도 도출할 수 있다.
      • 그리고 실제로 sin(2*pi*x)의 그래프는 멱급수 전개 상 M이 커질수록 성능이 단조 증가해야한다고 생각할 수 도 있다.
  • M에 따른 w* 값을 표로 그려보면 이 문제를 해결하는 데 도움이 될 것이다
    • M이 커질수록 w값은 점점 더욱 커진다.
    • 이것에 따라 M=9일때 피팅시킨 곡선을 보면 x가 커질수록 진동이 더욱더 커지게 된다.
    • 이것은 노이즈까지 정확하게 피팅시키게 된 결과이다.
  • 이러한 과는 데이터의 집합 크기가 커지면 과적합 문제가 완화된다.
    • 즉 다르게 말하면 데이터 집합이 클수록 복잡한 모델을 활용할 수 있다.
    • 또한 좋은 모델 훈련을 위해 매개변수(w값)들을 일정 숫자를 곱한 것이 경험적으로 좋을 수 있다.
      • regularization을 말하는 듯
  • 지금까지 설명한 것은(RMS 사용) 최대 가능도(maximum likelihood)의 방법론이다.
    • 하지만 베이지안(Bayesian) 방법론을 사용한다면 과적합 문제를 피할 수 있다.
    • 실제로 내가 모델을 구성할 때, M에 제약을 둔다는게 불만족스럽거나 애매할 수있기 때문에..
    • 이 두개의 차이는 책 뒷절에 나오게 되므로 일단 패스
  • 최대 가능도를 사용했을 때는 어떻게 해결해야할 까?
    • 대표적으로 정규화(regularization)가 있다.
    • 즉 loss에 penalty를 줘서 바꾸게 되는데..다음과 같다
    • 을 의미한다.
    • 추가적으로 w0은 을 구성할 때 빼고 w0 term은 따로 처리하기도 하는데, 이는 그래프의 원점에 관련된 것이기 때문이라고 하고 5.5.1절에서 논의한다고 함
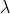    • 는 regularization의 중요도를 결정

연습 문제 1.2

  • 위의 새로운 regularization을 추가한 loss을 구성하는 방법은 수축법(shrinkage method)라고 한다.
    • 뉴럴 네트워크에서는 보통 weight decay라고 부름
  • 이유는 계수의 크기를 수축시키는 방법이기 때문이라고 한다.
  • 또한 이차 형식 정규화는 리지 회귀(ridge regression)이라고 부른다.

  • M=9 상황에서 ln을 변경시켜가면서 학습을 해본 결과를 보자
    • 표에서 =0인 것이 ln가 -무한대를 의미하고 가 커질수록 w*의 값은 줄어든다.
  • 실제로 모델 복잡도를 잘 선택할 때, 검증 집합(validation set, hold-out set)을 이용하여 결정할 수 있다.
    • 간단히 말하면, train 데이터로 모델을 학습하면서 validation 데이터에 얼마나 잘 맞추는지를 확인해 가면서 stop training을 하는 것이다.

댓글

댓글 쓰기