기본 콘텐츠로 건너뛰기
인공지능, AI, NLP, 논문 리뷰, Natural Language, Leetcode
PRML-01.2, 확률론
Introduction
- 확률론은 불확실성을 조작하기 위한 이론적인 토대이다. (패턴인식의 중요한 개념)
- 예시로 살펴 보자

- 조건) 빨강 상자를 고를 확률은 40%, 파랑 상자를 고를 확률은 60%, 그 안에서 각각의 과일을 고르는 확률은 같다고 하자.
- 앞으로의 전개에서 상자를 확률 변수 B라고 지칭한다.
- 즉 B는 r(빨강 상자)와 b(파랑 상자)를 가질 수 가 있다.
- 과일의 정체 역시 확률 변수 F라고 지칭한다.
- F는 a(사과)와 o(오렌지)의 값을 가질 수 있다.
- 무한 번 시도한다고 하였을 때 빨간색 상자를 고를 확률은 4/10, 파랑색 상자를 고를 확률은 6/10이 되고 이 두개의 확률을 합치면 1이 된다.
- 여기서 질문으로는 다음과 같은 것들이 있을 수 있다.
- '선택 과정에서 사과를 고를 전반적인 확률은 무엇인가?'
- '오렌지를 선택하였을 때, 우리가 선택한 상자가 파란색이었을 확률은 무엇인가?'
- 이러한 질문에 대한 답을 하려면 합의 법칙(sum rule)과 곱의 법칙(product rule)을 알아야 한다.
- 이 질문은 사실 고등 수준의 질문이지만 책에서는 다음의 예시를 추가적으로 들어서 이해를 돕는다

- 그림에서 X는 x_i(i=1~M), Y는 y_j(j=1~L)중 아무 값이나 취할 수 있다고 하자.
- X와 Y는 각각 표본을 N번 추출한다고 하자.
- X=x_i, Y=y_j인 시도의 개수를 n_ij로 표현하자.
- Y값과는 상관없이 X=x_i일 때 시도의 숫자를 c_i, X값과는 상관없이 Y=y_j일 때 시도의 숫자를 r_j로 표현하자.
- (여기서 말하고자 하는 것이 joint probability, conditional probability, marginal probability인 듯)
- X가 x_i, y가 y_j일 확률을
) 로 적고 이를
로 적고 이를  일 결합 확률(joint probability)라고 칭한다.
일 결합 확률(joint probability)라고 칭한다.
- 위에서 언급한 표기들을 이용하면 다음과 같이 된다.

- 비슷하게 Y값과 무관하게 X가 x_i값을 가질 확률은
) 으로 표기하고 다음과 같이 된다.
으로 표기하고 다음과 같이 된다.
-

 는 다음과 같으므로 식 1.6은 다음과 같이 표기할 수 있다
는 다음과 같으므로 식 1.6은 다음과 같이 표기할 수 있다
- 이를 합의 법칙(sum rule)이라고 하고
) 는 주변 확률(marginal probability)라고 부른다.
는 주변 확률(marginal probability)라고 부른다.
- X=x_i인 사례들만 고려했을 때, Y=y_j인 사례들의 비율을 생각해볼 수 있고 이를
) 로 적을 수 있고 이를 조건부 확률(conditional probability)라고 부른다.
로 적을 수 있고 이를 조건부 확률(conditional probability)라고 부른다.
- 위의 식들을(1.5, 1.6, 1.8)을 종합하여 다음과 같이 식을 표현할 수 있다.

- 이것을 확률의 곱의 법칙(product rule)이라고 한다.
- 이러한 표기법에 의해 과일 상자 B에서 상자가 빨강(r)일 확률을 p(B=r)으로 표기할 수 있다.
- 하지만 이러한 표현법은 실제 사용하기 번거롭다.
- 간단하게 확률 변수 B에서의 분포를 표현할 때는 p(B)로 적고 특정 값 r에서의 분포를 표현할 때는 p(r)로 적기로 하자! (즉 p(r)=p(B=r))
- 다시 한번 확률의 법칙을 정리하면)
- 합의 법칙:
&space;=&space;\sum_Y&space;p(X,Y))
- 곱의 법칙:
&space;=&space;p(Y|X)p(X))
- p(X, Y)을 읽을 때는 'X와 Y의 확률'이라고 읽으면 된다. (난 보통 'p X바 Y'라고 했던 것 같은데...)
- p(X)을 읽을 때는 'X의 확률'이라고 읽는다.
- p(X,Y)=p(Y,X)에서 부터 다음과 같은 식을 도출할 수 있다.

- 이를 베이즈 정리(Bayes' theorem)(매우중요⭐)이라고 한다. (머신러닝, 확률론에서 진짜 많이 쓰는 용어인 듯)
- p(X)을 합의 법칙으로 바꾸면 다음과 같이 식을 표현할 수도 있다.
=\frac{p(X|Y)p(Y)}{\sum_Yp(X|Y)p(Y)})
- 여기서 분모를 정규화 상수로 생각할 수도 있다.

- 위 그림은 앞서 말했던 것들에 대한 예시라고 볼 수 있다.
- 확률 분포, 조건부 확률, marginal 확률 등에 대한 그래프들 이있다.
- 이제 초기 과일 상자 예시로 돌아가서 다시 설명을 한다.
- p(B=r) = 4/10, p(B=b) = 6/10 인 상황
- 맨 처음 그림을 참고하면 다음과 같은 조건부 확률 결과를 도출할 수 있다.
- p(F=a|B=r) = 1/4
- p(F=o|B=r) = 3/4
- p(F=a|B=b) = 3/4
- p(F=a|B=b) = 1/4
- 이를 확률의 합과 곱의 법칙을 이용하여 다음과 같이 사과를 고를 확률을 구할 수 있다.
- p(F=a) = p(F=a|B=r)p(B=r) + p(F=a|B=b)p(B=b) = 1/4*4/10 + 3/4*6/10 = 11/20
- 이를 통해 p(F=o) = 1-11/20 = 9/20 임을 알 수 있다.
- 만약 내가 고른 과일이 오렌지고 이 오렌지가 어떤 상자에서 나왔는지를 알고 싶은 상황은 다음과 같다.(베이지안 정리에 의해)
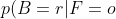=\frac{p(F=o|B=r)p(B=r)}{p(F=o)}=\frac{3}{4}\times&space;\frac{4}{10}&space;\times&space;\frac{20}{9}&space;=&space;\frac{2}{3})
- 합의 법칙에 따라 p(B=b|F=o)=1-2/3=1/3
- 베이지안 정리가 왜중요한지 이 책에서도 언급을 한다.
- 만약 어떤 과일이 선택되었는지를 알기 전에 어떤 박스를 선택했냐고 묻는다면 그 확률은 p(B)의 값이다.
- 이를 사전 확률(prior probability)라고 부른다.
- 하지만 선택한 과일이 오렌지라는 것을 알게 된다면 베이지안 정리르 활용하여 p(B|F)를 구할 수 있고 이를 사후 확률(posterior probability)라고 부른다.
- 위의 예시에서 고른 과일을 모른다면 파랑 상자를 고를 확률이 60%이기 때문에 파랑상자일 확률이 높다.
- 하지만 오렌지를 고른 상황이 주어지면 빨강 상자를 고를 확률이 2/3이기 때문에 빨강상자일 확률이 높은 것으로 바뀌게 된다.
- 아마 책 뒷 부분에서 나올 것 같은데 대학원 수업때 생각해보면 정보(label 등)이 주어지고 어떤 feature 분포에서 뽑힌 data냐? 이런 관점에서 패턴인식을 접근하는 것으로 기억한다.
- p(X,Y)=p(X)p(Y)인 경우 처럼 각각의 주변 확률을 곱한 것이 결합 확률이 되는 경우 두 확률 변수를 독립적(independent)라고 한다.
- 곱의 법칙 식과 비교해보면 p(Y|X) = p(Y)라는 말과 똑같고 이는 X의 값이 Y의 조건에 상관이 없다는 것이다.
1.2.1 확률 밀도
- 실수 변수 x가
) 구간 안의 값을 가지고 그 변수의 확률이
구간 안의 값을 가지고 그 변수의 확률이 \delta&space;x(\delta&space;x&space;\rightarrow&space;0)) 로 주어지면 p(x)를 x의 확률 밀도(probability density)라고 부른다.
로 주어지면 p(x)를 x의 확률 밀도(probability density)라고 부른다.
- 확률 밀도라는 개념을 만약 모르고 이 문장만 봐서는 사실 와닿는 표현은 아니라고 생각하지만 확률 밀도는 고등수학에서도 나오는 개념이기 때문에 혹시라도 모르신다면 인터넷 검색 ㄱ..
 (그림 1.12)
(그림 1.12)
- 식으로 표현하면 다음과 같다.
)&space;=&space;\int_{a}^{b}&space;p(x)dx)
- 이 때 확률이라는 개념으로 인해 다음과 같은 조건이 붙는다.
- 확률 분포 함수는 야코비안 인자로 비선형 변수 변환 시에 다음과 같이 변환한다.
- x=g(y)의 변수 변환에 대해서 x의 확률 밀도 함수
) 와
와 ) 를 살펴보자
를 살펴보자
) 범위에 속하는 값은
범위에 속하는 값은 ) 으로 변환될 것이다.
으로 변환될 것이다.=p_x(x)|\frac{dx}{dy}|=p_x(g(y))|g'(y)|)
- x가
) 범위에 속할 확률은 누적 분포 함수(cumulative distribution function)으로 표현된다.
범위에 속할 확률은 누적 분포 함수(cumulative distribution function)으로 표현된다.
=\int_{-\infty}^{z}p(x)dx)
- 그림 1.12에서 위 식을 미분했을 떄의 결과인 P'(x)=p(x)가 됨을 유추할 수 있다.
- 만약 연속적인 변수
 가 주어지고 이변수들이 벡터
가 주어지고 이변수들이 벡터 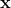 로 주어질 때 결합 확률 밀도 (joint probability)
로 주어질 때 결합 확률 밀도 (joint probability) =p(x_1,&space;\cdots,&space;x_D)) 를 다음과 같이 정의할 수 있다.
를 다음과 같이 정의할 수 있다.
&space;\geqslant&space;0)
d\textbf{x}=1)
- 위의 적분은 전체 x 공간에 대해 적분한다는 것


로 적고 이를
일 결합 확률(joint probability)라고 칭한다.
으로 표기하고 다음과 같이 된다.
로 적을 수 있고 이를 조건부 확률(conditional probability)라고 부른다.


구간 안의 값을 가지고 그 변수의 확률이
로 주어지면 p(x)를 x의 확률 밀도(probability density)라고 부른다.
 (그림 1.12)
(그림 1.12)




댓글
댓글 쓰기