NL-077, Linformer: Self-Attention with Linear Complexity (2020-Preprint)
■ Comment
- 이 논문은 Reformer보다 더 어렵게 느끼게 수학적인 것이 많다.
- 논문의 목적은 Reformer처럼 pretrained 모델은 워낙 방대해서 학습할 때, 좀 효율적으로 적은 메모리와 시간 복잡도를 가지도록 학습하고 싶은 것이다.
- Reformer보다 좋은 방법이지만, 실질적으로 reformer은 시퀀스 길이가 2048이 넘어가야 효율성이 느껴진다고 한다는 단점이 있다.
- 따라서 Linformer은 시퀀스 길이 n에따라 선형적인 복잡도를 가지도록 하는 목표를 가지고 있다.
- 아주 간단히 말하면 방법론은 식 7이 대표성을 띄고 self-attention의 K, V에 각각 저차원으로 보내는 projection linear matrix을 곱하여 진행한다는 것이다.
- 이렇게 해도 성능이 보존되는 projection matrix의 존재 유무를 수학적으로 증명을 하기 때문에 논문이 어려운 것이다.
- 수식적으로 증명하는 과정을 이해하면, 이후에 어떤 새로운 아이디어를 얻기 위하여 수학적인 접근하는 능력이 오르겠지만...
- 대부분 이런 목적이 최우선인 사람은 별로 없을 것이다.
- 즉 증명 이해하는데 가성비 측면에서 떨어진다고 생각하여 패스하였으나 필요한 사람들은 화이팅..
- 물론 실험적으로도 성능이 보존됨을 보여준다.
- 1) 여기서 언급한 방법으로는 SVD을 통하여 eigenvalue을 이용하는 방법
- 2) 단순 linear matrix을 곱하는 방법
- 3) Convolution(mean, max pooling 등) 방법
- 이 있는데 2번 방법을 논문에서는 사용하였다.
- 추가적인 스킬로는 Parameter sharing between projections와 Nonuniform projected dimension 등이 있다.
- 즉 ALBert처럼 E, F등의 파라미터를 공유하는 방법과
- projection 시킬 차원을 공통된 값이 아닌 것을 사용하는 것이다.
- 결과적으로 성능이 유지되면서 적은 메모리와 시간의 복잡성을 가진다.
- 이 논문을 읽고 든 생각은
- 엔비디아글에 보면 다음과 같이 써있다.
- BERT는 논문에서 제시된 구성에 따라 BERT-Large 모델을 Tesla V100 32G * 8 GPU 서버 한 대로 Pre-training시, 약 2주간 학습이 필요한 무거운 모델입니다.
- 이 논문에서 학습할 때는 V100 64개, 인퍼런스는 V100 1개를 쓴 것 같다.
- 다른 pretraining 모델과 공정하게 비교하려고 V100 64개를 쓴 것 같지만, 정말 Linformer을 학습하기 위한 최대한 적은 V100 개수에 대한 언급은 없는게 아쉽다.
- 차라리 어떻게 보면, 기존의 대규모 코퍼스 학습된 모델을 적은 GPU로 distillation하는 것이 효율적인 게 아닐까? 싶다.
0. Abstract
- 큰 transformer models은 놀라울 성공을 보여주며 많은 NLP 어플리케이션에서 SoTA
- 그러나, 이러한 모델들은 학습과 적용을 하는 것은 긴 문장에 대해 비용이 못할 정도로 비싸고 standard self-attention Transformer 메커니즘은 O(n2)(n=시퀀스 길이) 시간과 공간을 가진다.
- 이 논문에서, 우리는 self-attention 메커니즘이 low-rank 행렬로 근사화할 수 있음을 보여준다.
- 우리는 게다가 새로운 self-attention 메커니즘을 찾아서 전체 self-attention 복잡도를 O(n2)에서 O(n)으로 시간과 공간을 줄인다.
- 그 결과 linear transformer인 Linformer은 standard Transformer 모델과 동등한 성능을 가지고 메모리와 시간 효율성이 훨씬 효율적이다.
1. Introduction
- Transformer 모델들은 NLP에서 다양한 문제들에서 (번역, 분류, QA, 다른 것들) 어디에나 존재한다.
- 최근동안, 많은 수의 파라미터를 가지는 SoTA NLP transformers은 급격히 늘어났고 기존 340 million (=340*10^6) 파라미터를 가지는 BERT-Large에서부터 175 billion개 (=175*10^9)를 가지는 GPT-3까지 있다.
- 이러한 큰 스케일의 모델들은 인상적인 결과를 다양한 태스크에서 보여주지만, 각 모델의 학습과 적용은 실제 느리다.
- 예를 들어, 기존의 BERT-Large 모델은 4일을 16 Cloud TPUs으로 학습하고 최근 GPT-3은 이전 GPT-2에 비해 petaflops/일 을 훨씬 많이 계산한다.
- 학습 위에서, Transformer 모델들을 실제 세계에 적용하는 것은 비용이 비싸고, 보통 extensive distillation 혹은 comrpession 을 해야한다.
- Transformer의 메인 효율성 바틀낵은 자신의 self-attention 메커니즘이다.
- 여기서 각 토큰의 representation은 이전의 layer에서 다른 tokens을 attending하여 업데이트 된다.
- 이 작업은 long-term information을 유지하는 key이고 Transformers가 긴 시퀀스에서 RNN모델을 넘어서게 한다.
- 그러나, 모든 토큰들을 각 layer에서 attending 하는 것은 시퀀스 길이에 관해서 O(n2)의 복잡도를 가진다.
- 그래서, 이 논문에서 우리는 질문에 대한 정답을 찾았다.
- 질문: Transformer 모델은 이 quadratic operation을 피하고 최적화 될 수 있거나 이 operation이 강한 성능을 유지하는데 필요한가?
- 위 질문에 대해 답을 찾는 것이 이 논문의 핵심
- 이전의 연구에서 여러 개의 테크닉으로 self-attention의 효율성을 향상시킨다.
- 한 가지 유명한 테크닉은 sparsity 을 attention layers에 넣는 것인데, 각 토큰이 오직 전체 시퀀스의 토큰 부분집합에 대해서만 attend 하는 것이다. (바로 전에 읽은 Reformer 방법)
- (Child et al., 2019) 이것은 전체 attention 메커니즘을 복잡도 O(n
)
- 그러나 Qiu et al. (2019)에서는 이 방법이 제한된 효율성을 가지고 큰 성능 하락으로부터 고통을 받는다. (i.e., a 2% drop with only 20% speed up.)
- 좀 더 최근에는, Reformer은 locally-sensitive hashing (LSH) 을 사용하여 복잡도를 O(nlog(n))으로 낮춘다.
- 그러나 실제로, Reformer 효율성 이득은 오직 길이가 2048을 넘어가는 시퀀스에서 나타난다 (Figure 5 in Kitaev et al. (2020)).
- 게다가, Reformer의 multi-roung hashing 접근법은 실제로 많은 병렬젹 계산의 수를 늘려서 최종 효율적 이득을 떨어뜨린다.
- 이 연구에서, 우리는 새로운 접근법으로 Transformer의 self-attention 바틀낵을 다룬다.
- 우리의 접근법은 self-attention이 low rank인 key observation으로부터 영감을 받았다.
- 좀 더 정확하게, 우리는 이론적과 경험적으로 self-attention의 형태인 stochastic matrix가 low-rank matrix로 근사화될 수 있음을 보여준다.
- 이러한 강력한 관찰로부터, 우리는 새로운 메커니즘으로 self-attention을 space와 time 복잡도 모두를 O(n) operation으로 줄인다
- 우리는 기존의 scaled dot-product attention을 multiple linear projections을 통하여 smaller attention으로 분해한다.
- 그래서 이러한 operations의 조합은 기존 attention의 low-rank으로 factorization을 형성한다.
- A summary of runtimes for various Transformer architectures, including ours, can be found in Table 1.
- 한 가지 Transformers의 주요 어플리케이션은 가장 큰 이득을 얻는 것은 pretrained language models을 사용하는 것이다.
- 반면에 모델들은 먼저 큰 코퍼스로 language modeling으로 pretrained 되어야 한다.
- 그리고나서 supervised data을 사용하여 target tasks에 finetuned 된다.
- Devlin et al. (2019)에 따르면 우리는 우리의 모델을 BookCorpus+English Wikipedia로 masked-language-modeling objective을 사용하여 pretrain 한다.
- 우리는 기존의 Transformer 모델과 비슷한 pretraining 성능을 보여준다.
- 우리는 그리고나서 우리의 pretrained models을 3가지 tasks인 GLUE, Sentiment analysis, IMDB reviews에서 finetune한다.
- 이러한 태스크에서, 우리의 모델은 비교적, 기존의 pretrained Transformer에 비해 학습과 인퍼런스 스피드는 빨라지면서 성능은 약간 좋아진다.
2 Backgrounds and Related works
2.1 Transformer and Self-Attention
- Transformer은 너무 유명하기 때문에 간단히 수식만 보고 넘어가는 걸로..
- 다들 알다시피 Multi-Head Self-Attention (MHA)을 기반으로 진행이 된다.
- 여기서 P가 nxn 차원의 행렬로 self-attention을 의마한다.
- 이 P가 계산 비용이 많이 들고 O(n2)의 time과 space 복잡도를 가진다.
- This quadratic dependency on the sequence length has become a bottleneck for Transformers.
2.2 Related works
- Mixed Precision (Micikevicius et al., 2017)
- (floating point) 부동 소수점의 half-precision or mixed-precision representations을 사용하는 것은 딥 러닝에서 널리 사용되며 Transformers 훈련에도 널리 사용됩니다 (Ott et al., 2019).
- Knowledge Distillation (Hinton et al., 2015)
- Knowledge distillation aims to transfer the “knowledge" from a large teacher model to a lightweight student model.
- 단점: 교육 과정에서 교사 모델의 속도를 높이는 것은 아니며, 학생 모델은 일반적으로 교사 모델에 비해 성능이 저하됩니다.
- Sparse Attention (Child et al., 2019)
- 이 기법은 컨텍스트 매핑 행렬 P에 희소성을 추가하여 자기 집중의 효율성을 향상시킵니다.
- 예를 들어, Sparse Transformer (Child et al., 2019)는 모든 Pij 대신 행렬 P의 대각선 주위에서만 Pij를 계산합니다.
- 그러나, 이러한 기술들은 또한 추가적인 추가적인 속도 향상, 즉 20 % 속도로 2 % 감소를 제한하면서 큰 성능 저하를 겪는다.
- LSH Attention (Kitaev et al., 2020)
- self-attention complexity을 O(n log(n))으로 줄여준다.
- 그러나, 실제로 their complexity term has a large constant 128^2 and it is only more efficient than the vanilla transformer when sequence length is extremely long
- Improving Optimizer Efficiency
- 마이크로바칭(Huang et al., 2019)은 한 묶음을 작은 마이크로배치(메모리에 맞을 수 있음)로 나눈 다음, 구배 축적과 함께 그 위에서 앞뒤 패스를 따로 실행한다.
- 그라데이션 체크포인트(Chen et al., 2016)는 레이어의 서브셋 활성화만 캐싱하여 메모리를 절약한다.
- 캐시되지 않은 활성화는 최신 체크포인트에서 백프로포즈하는 동안 다시 계산된다. 두 가지 기술 모두 기억력과 오프 타임(Off-time)을 교환하며, 추론 속도를 높이지 않는다.
3 Self-Attention is Low Rank
- 이 섹션에선, 우리는 self-attention 메커니즘, contet mapping matrix P이 low-rank 임을 입증한다.
- 우리는 먼저 context mapping matrix P의 스펙트럼 분석을 제공한다.
- 우리는 pretrained transformer models, RoBERTa-base (12-layer stacked transformer) and RoBERTa-large (24-layer stacked transformer) (Liu et al., 2019)을 2가지 태스크에 사용한다.
- masked-language-modeling task on Wiki103 (Merity et al., 2016)
- classification task on IMDB (Maas et al., 2011).
- 그림 1 왼쪽에서 우리는 SVD을 P의 다른 layers와 모델의 다른 heads에 적용하고 10k 문장들에 관하여 noramlized cumulative singular value을 평균내서 그려본다.
- 결과는 각 layer, head 및 태스크에 걸쳐 명확한 long-tail spectrum 분포를 나타냅니다.
- 이는 행렬 P의 대부분의 정보가 처음 몇 개의 가장 큰 singular values에서 복구 될 수 있음을 의미합니다.
- 그림 1의 오른쪽에서는, we plot a heatmap of the normalized cumulative singular value at the 128-th largest singular value (out of 512).
- 그림 1 (오른쪽)에서 higher layers의 스펙트럼 분포가 lower layers보다 왜곡되어 있음을 알 수 있습니다.
- 이는, higher layers에서는 더 많은 정보가 가장 큰 singular values에 집중되고 P의 순위는 더 낮습니다.
- 이제 할 것은 이것을 이론적으로 분석한다!!
- 위 정리를 글로 쓰자면, Q, K, V (n x d)의 어떤 행렬과
,
,
(d x d)가 주어졌다고 하자.
- n은 시퀀스 길이이고 d는 dimmension의 표기일 것이다.
- 이때 V
- 어떠한 w에 대해서도 ||
-P
||P
)=
(log(n))이 되도록 하는
- 참고로 P는 식2에서 QK^T을 의미하여 V에 곱하는 것이다.
- 즉, 위 정리는 (QK^T)V을 할 때, QK^T 대신에
- 위 정리를 증명하는 것은 굳이 이해할 필요가 있나 싶다..
- 논문에 간략히 써있지만 자세히는 보충자료까지 봐야하므로..
- 궁금한 사람은 직접 보도록!
- low-rank property of the context mapping matrix P가 주어질 때, 간단한 한 가지 아이디어는 다음과 같이 단일 값 분해 (SVD)를 사용하여 P를 low-rank 행렬 Plow로 근사화하는 것입니다.
- where σi , ui and vi are the i largest singular values and their corresponding singular vectors.
- 즉 singular values가 큰 몇 개를 사용하는 것으로 일반적인 SVD로 정보 압축하는 것
- 얼굴인식에서 PCA 등과 같은 개념임.
- 근데 아무튼 이렇게 했을 때, P_low는 self-attention을
- 시간 복잡도를 생각해보면
- 원래 행렬 계산은 Q=(n x d), K=(d x n), V=(n x d)이 주어지고 P을 계산할 때 (n x d) x (d x n)으로 (n x n)을 계산할 때 복잡도 O(n^2)가 필요하고 P x V을 계산할 때는 (n x n) x (n x d)이므로 복잡도는 O(n^2)이다.
- 그런데, 위와 같이 P_low로 차원을 줄이고 보면(ui, ki는 n차원 vector이므로 ) P_low = (n x k) x (k x k) x (k x n) = n x n을 계산할 때 복잡도는 O(nk)이기 때문에 복잡도가 줄어든다는 것 같다.
- 물론 P_low x V할 떄는 복잡도가 똑같이 O(n^2)가 든다.
- 공간 복잡도를 생각해보면
- 저장되는 공간이므로 직관적으로 O(n^2) P 행렬이 O(nk)인 P_low로 줄어들게 된다.
- 참고로 행렬 (a x b) x (b x c)을 계산할 때 복잡도는 O(abc)인데 위에서는 d를 생략하는 것이다.
- 하지만 이 방법은 SVD을 self-attention에 수행해야기 때문에 추가적인 복잡성을 요구하게 된다.
- 따라서 여기서는 다른 방법으로 low-rank approximation으로 추가적인 복잡성을 피해준다.
4 Model
- 이 섹션에서는, 우리는 새로운 self-attention 메커니즘으로 시퀀스 길이에 관해 linear time과 memory 복잡성을 가지는 contextual mapping P*V
- 그림2처럼 linear self-attention의 메인 아이디어는 key와 value을 계산할 때, 두 개의 linear projection 행렬인 Ei, Fi (n x k)을 추가한다.
- 우리는 먼저, original (n x d) 차원의 key와 value layers K
- 우리는 그리고나서 scaled dot-product attention을 사용하여 n x k 차원의 context mapping matrix
을 계산한다.
- 결국, 우리는 각 head_i의 context embeddings을
- 위의 계산은 오직 O(nk)의 time과 space 복잡성이 든다.
- 따라서, 우리가 만약 매우 작은 차원 k인 k << n으로 사영시킨다면, 우리는 많은 메모리와 공간 소비를 절약할 수 있다.
- 다음의 정리는 k=O(d/
- 식 수식을 보면 알겠지만, w는 여기서
- k을 min{
- 쉽게 말해서, k을 잘 선택해주면 기존의 식과 차이가 안나는 Ei, Fi 가 존재한다!
- 이것도 마찬가지로 증명은 패스...
- 그림 2의 오른쪽에서 우리는 Linformer의 inference 속도와 standard Transformer을 시퀀스 길이에 관해 비교한다. (전체의 tokens의 수는 고정시키고)
- standard 트랜스포머가 긴 시퀀스 길이에서는 느리지만, Linformer 속도는 비교적 평탄하게 유지되고 긴 시퀀스에서는 현저하게 더 빠르다는 것을 알 수 있다.
- Additional Efficiency Techniques
- 성능 및 효율성 모두에 대해 더욱 최적화하기 위해 Linfilteron 위에 몇 가지 추가 기술을 도입할 수 있다.
- Parameter sharing between projections:
- Linear projection matrix Ei , Fi에 대한 파라미터를 layer와 heads에 걸쳐 공유할 수 있다.
- 특히 다음과 같은 3가지 level에서 공유를 실험했다.
- Headwise sharing:
- for each layer, we share two projection matrices E and F such that Ei = E and Fi = F across all heads i.
- Key-value sharing:
- we do headwise sharing, with the additional constraint of sharing the key and value projections.
- For each layer, we create a single projection matrix E such that Ei = Fi = E for each key-value projection matrix across all head i.
- Layerwise sharing:
- we use a single projection matrix E across all layers, for all heads, and for both key and value.
- 즉 위에서부터 아래로 갈수록 공유의 정도?가 더 많아지는 것
- 약간 ALBert에서 말하는 개념의 느낌
- For example, in a 12-layer, 12-head stacked Transformer model, headwise sharing, key-value sharing and layerwise sharing will introduce 24, 12, and 1 distinct linear projection matrices, respectively.
- Nonuniform projected dimension:
- 다른 heads와 layers에 대해 다른 projected dimension k를 선택할 수 있다.
- 그림 1(오른쪽)에서 보듯이, 서로 다른 heads와 layers의 contextual mapping matrices는 구별되는 스펙트럼 분포를 가지며, 상위 layers의 heads는 더 왜곡된 분산 스펙트럼(하위 순위)을 지향하는 경향이 있다.
- This implies one can choose a smaller projected dimension k for higher layers.
- General projections:
- 또한 simple linear projection 대신 다양한 종류의 low-dimensional projection을 선택할 수 있다.
- 예를 들어, mean/max pooling 또는 kernel 과 stride 이 n/k로 설정된 convolution을 선택할 수 있다.
- convolutional functions은 훈련을 필요로 하는 매개변수를 포함한다.
5 Experiments
5.1 Pretraining Perplexities
- All models are pretrained with the masked-language-modeling (MLM) objective, and the training for all experiments are parallelized across 64 Tesla V100 GPUs with 250k updates.
- 그래프만 봐서는 Linformer와 standard와 큰 차이가 없어보인다.
- 오른쪽 아래가 좀 차이가 두드러져보이는데, n이 클수록(시퀀스가 길수록) 학습이 되는 속도는 느리지만, 최종 수렴점은 비슷하다는 것을 보여준다.
- 이것이 논문에서는 Linformer가 linear-time라는 가정을 뒷받침한다고 한다.
5.2 Downstream Results
- 표의 수치들을 보면 느낌이 오듯이 숫자가 큰 차이가 없다라는 것이 느껴진다.
5.3 Inference-time Efficiency Results
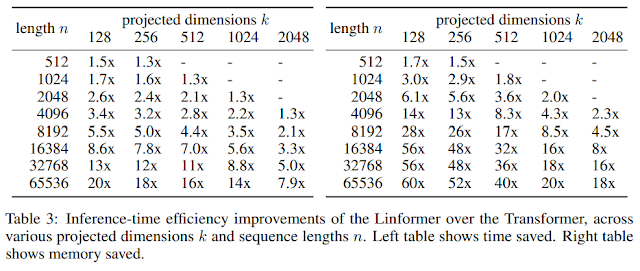
- k와 n을 다양한 값을 가지게 함으로써 실험을 하면서 inference 시간을 비교했다.
- k가 작고 n이 커질수록 시간과 메모리가 절약된다.
- In Table 3, we report the inference efficiencies of Linformer (with layerwise sharing) against a standard Transformer.
- We benchmark both models’ inference speed and memory on a 16GB Tesla V100 GPU card.
6 Conclusion
- Transformer 모델들은 self-attention operations이 시퀀스 길이 n에 대하여 O(n^2)의 time, space 복잡성을 가지기 때문에 학습과 적용이 느리기로 악명이 있다.
- 이 논문에서는, 우리는 이론적으로 경험적으로 self-attention으로 형성된 stochastic matrix가 low-rank의 형태를 가진다는 것을 보여준다.
- 우리는 더 나아가서, 새롭고 높은 효율을 가지는 self-attention 메커니즘을 제안한다.
- 이론적, 경험적 분석의 조합을 통하여, 우리는 우리의 접근법이 시퀀스 길이에 관하여 O(n)을 가지는 것을 보여준다.
Reference
댓글
댓글 쓰기