기본 콘텐츠로 건너뛰기
인공지능, AI, NLP, 논문 리뷰, Natural Language, Leetcode
랭킹, 추천 평가메트릭
백그라운드
- 클래스가 총 10개라고하자.

- True Positive(TP) : 실제 True인 정답을 True라고 예측 (정답)
- False Positive(FP) : 실제 False인 정답을 True라고 예측 (오답)
- False Negative(FN) : 실제 True인 정답을 False라고 예측 (오답)
- True Negative(TN) : 실제 False인 정답을 False라고 예측 (정답)
- 즉 앞에 True가 있으면 맞춘 것을 의미, 뒤는 예측 레이블을 의미
- precision = TP/(TP+FP)
- recall = TP/(TP+FN)
- 참고문서:
precision
- precision은 True로 예측한 것 중 실제 True가 몇개?라는 컨셉이다
- 일반적으로 precision 자료를 찾아보면 binary classification에서 예를 드는 경우가 많다.
- 바이너리인 경우는 인터넷 자료를 보면 쉽게 이해가 될 것이다.
- 하지만 실질적으로는 멀티 클래스인 경우가 많다.
- 즉 이럴 때는, 각 클래스에 대해 precision을 계산하면 된다.
- 예시에서 클래스가 10개라고 했다
- 그럼 1번클래스=True, 나머지클래스=False 이라고 간주하여 각 테스트데이터에대해 precision을 계산하면 된다.
- 그 다음, 각 클래스에 대한 precision을 평균내주면 최종 precision이 된다.
- https://ai-creator.tistory.com/579
- 멀티레이블인 경우는 보통 precision@k을 사용한다.
- 감정인식으로 예를 들어보자.
- 감정클래스=(기쁨,슬픔,화남,즐거움,중립,지루함)
- 입력문장: 오늘 놀이동산 와서 정말 신난다!
- 실제정답: 기쁨, 즐거움
- 예측확률: 기쁨, 슬픔 , 화남, 즐거움, 중립, 지루함 (순서대로 높은확률)
- 이때 p@k을 계산해보자
- p@1 = 1
- p@2 = 1/2
- p@3 = 1/3
- p@4 = 2/4
- p@5, p@6 = 2/5, 2/6
- 이렇게 된다고 이해하면 된다.
- p@k도 각 테스트데이터에 대해 계산하고 이를 평균내주면 최종 p@k가 된다.
recall
- recall은 실제 True중 맞춘 것이 몇개?라는 컨셉이다.
- 나머지는 precision과 똑같다.
- r@k는 비교적 사용하는 경우를 잘 못봤다
- 즉, 정답이 4개인 경우 r@3는 3개를 정답으로 예측했는데 이중 정답이 몇개 겹치냐?를 의미한다.
- 따라서 precision과 달리, k에 상관없이 분모가 고정이 된다.
fscore
- 이는 precision 과 recall 의 기하평균이라고 보면된다.
- F = 2*(p*r)/(p+r)
- p@k와 r@k을 이용해서 각 데이터에 대해 Fscore을 구해서 평균내면 데이터의 fscore이다.
- 이는 사실 sklearn 함수 라이브러리에 있는걸 사용하면 된다.
macro, micro, weighted 차이
- https://data-minggeul.tistory.com/11
MRR (Mean Reciprocal Rank)
- 상위 1개에 집중하는 개념
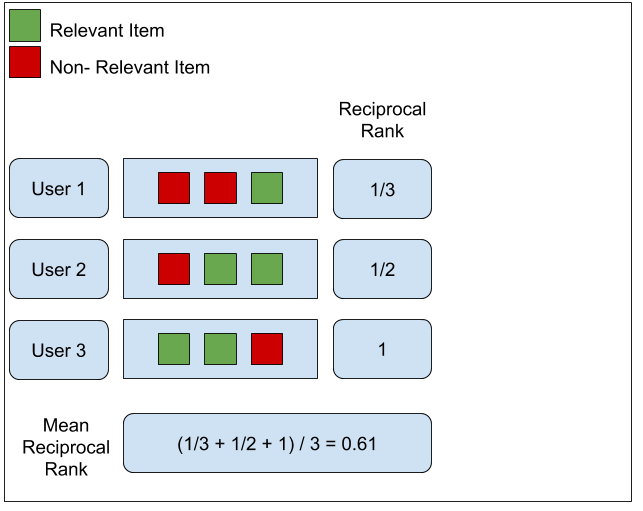
- 즉 관련있는 item이 언제나오냐가 핵심
- 이를 통해 각각 reciprocal rank을 구하고, 이를 평균내는게 mean reciprocal rank = MRR이 된다.
- MRR의 장점
- 간단하고 쉽다.
- 제공된 목록 중 가장 상위의 관련된 컨텐츠에만 집중하기 때문에, 사용자에 가장 관련있는 컨텐츠가 최상위에 있는가를 평가할 때 용이하다.
- 새로운 컨텐츠가 아니라 이미 사용자가 알고 있는 컨텐츠 중 가장 선호할만한 컨텐츠를 보여주고자 할 때 좋은 평가 기준이 된다.
- MRR의 단점
- 제공된 목록 중 하나의 컨텐츠에만 집중하기 때문에 나머지 부분에 대해서는 평가하지 않는다.(2, 3번째 관련 컨텐츠에 대해서는 평가를 하지 않는다.)
- 관련 컨텐츠의 개수가 달라도 첫 번째 관련 컨텐츠의 위치가 같은 경우 같은 점수를 가지므로 변별력을 가지기 어렵다.
- 사용자가 컨텐츠에 대해 잘 알지 못해 여러 번 탐색을 해야 하는 경우 살펴봐야 하는(관련있는) 컨텐츠의 개수가 1개 이상일 가능성이 높으므로 좋은 평가 기준이 되기 어렵다.
MAP (Mean Average Precision)
- p@k는 MRR와 달리 여러 개의 레이블을 고려할 수 있지만 다음의 단점이 있다.
- 상위 N개까지의 정밀도를 구하는 것(Precision@N)이다. 이 방법은 관련된 컨텐츠의 개수를 점수에 반영할 수 있다는 장점이 있지만, 관련된 컨텐츠의 위치(rank)를 점수에 반영할 수 없다는 문제점이 있다.
- 즉 p@k 위치 점수를 반영할 수 없다.
- 이의 문제를 해결하는 방법으로 MAP(Mean Average Precision)
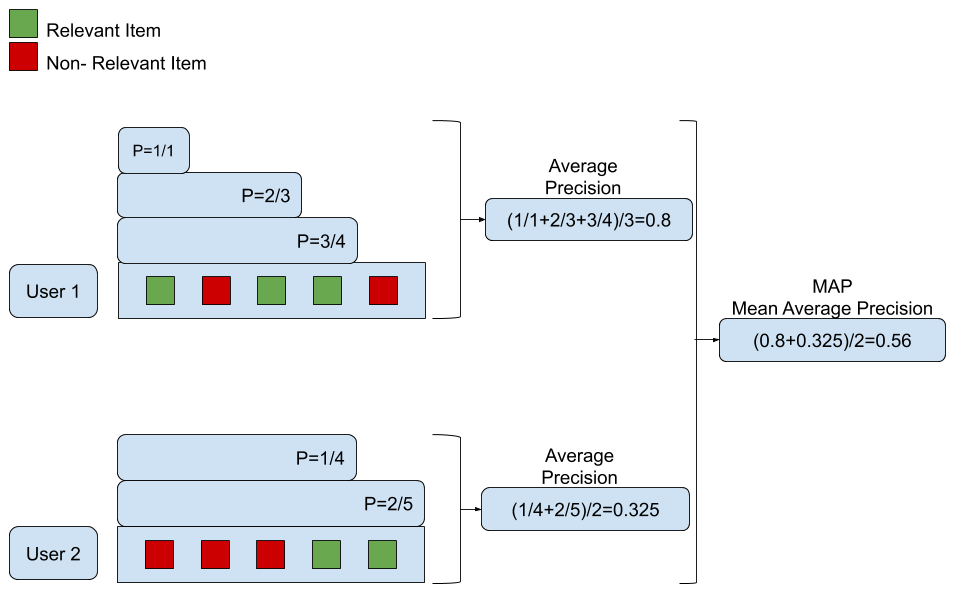
- 이 예에서는 사용자 2명에게 각각 5개의 추천 컨텐츠를 평가 대상으로 삼는다.
- 사용자 1의 경우 1,3,4번째 컨텐츠가 관련 컨텐츠이고, 사용자 2의 경우 4,5번째 컨텐츠가 관련 컨텐츠인 것을 확인할 수 있다.
- 사용자 1에 대해 평균 정밀도(average precision)을 계산하면 첫 번째 관련 컨텐츠까지 정밀도가 1/1 = 1이고, 다음 관련 컨텐츠인 세 번째 관련 컨텐츠까지 정밀도는 2/3(총 3개 중 2개가 관련된 컨텐츠)이다.
- 동일한 방법으로 네 번째 컨텐츠까지의 정밀도는 3/4이다.
- 이 3개의 정밀도 값 평균을 내면 사용자 1의 평균 정밀도인 (1/1+2/3+3/4)/3 = 0.8이 된다.
- 동일한 방법으로 사용자 2에 대한 평균 정밀도를 구하면 (1/4+2/5)/2 = 0.325가 된다.
- 이렇게 구해진 각 사용자의 평균 정밀도에 대하여 평균을 구하면 (0.8 + 0.325)/2 = 0.56이 되고 이 값이 해당 IR의 MAP 점수가 된다.
- 쉽게 생각해서 각 relevant 위치에서 p@k을 계산하고, 이를 평균낸 것 = average precision
- 각 데이터에 대해 전체평균낸 것 = MAP
- MAP 장점
- 추천 컨텐츠의 단순한 성능을 평가하는 것이 아니라 우선순위를 고려한 성능을 평가할 수 있다.
- 상위에 있는 오류(관련없는 컨텐츠)에 대해서는 가중치를 더 주고, 하위에 있는 오류에 대해서는 가중치를 적게 주어 관련 컨텐츠가 상위에 오를 수 있도록 도움을 준다.
- MAP 단점
- MAP는 관련 여부가 명확하지 않은 경우에는 계산하기 어렵다.
- 1~5점으로 평가하는 평점같이 관련 여부를 판단하기 어려운 경우는 MAP를 사용하기 어렵다.(4~5점은 관련있다고 판단하더라도 3점은 관련 여부를 판단하기 어려울 것이다.)
NDCG (Normalized Discounted Cumulative Gain)
- NDCG는 관련 여부에 대해 이분법적으로 구분하는 것이 아니라 더 관련있는 컨텐츠는 무엇인가?에 대해 집중하여 더 관련있는 컨텐츠를 덜 관련있는 컨텐츠보다 더 상위에 노출시키는지에 대해 평가한다.
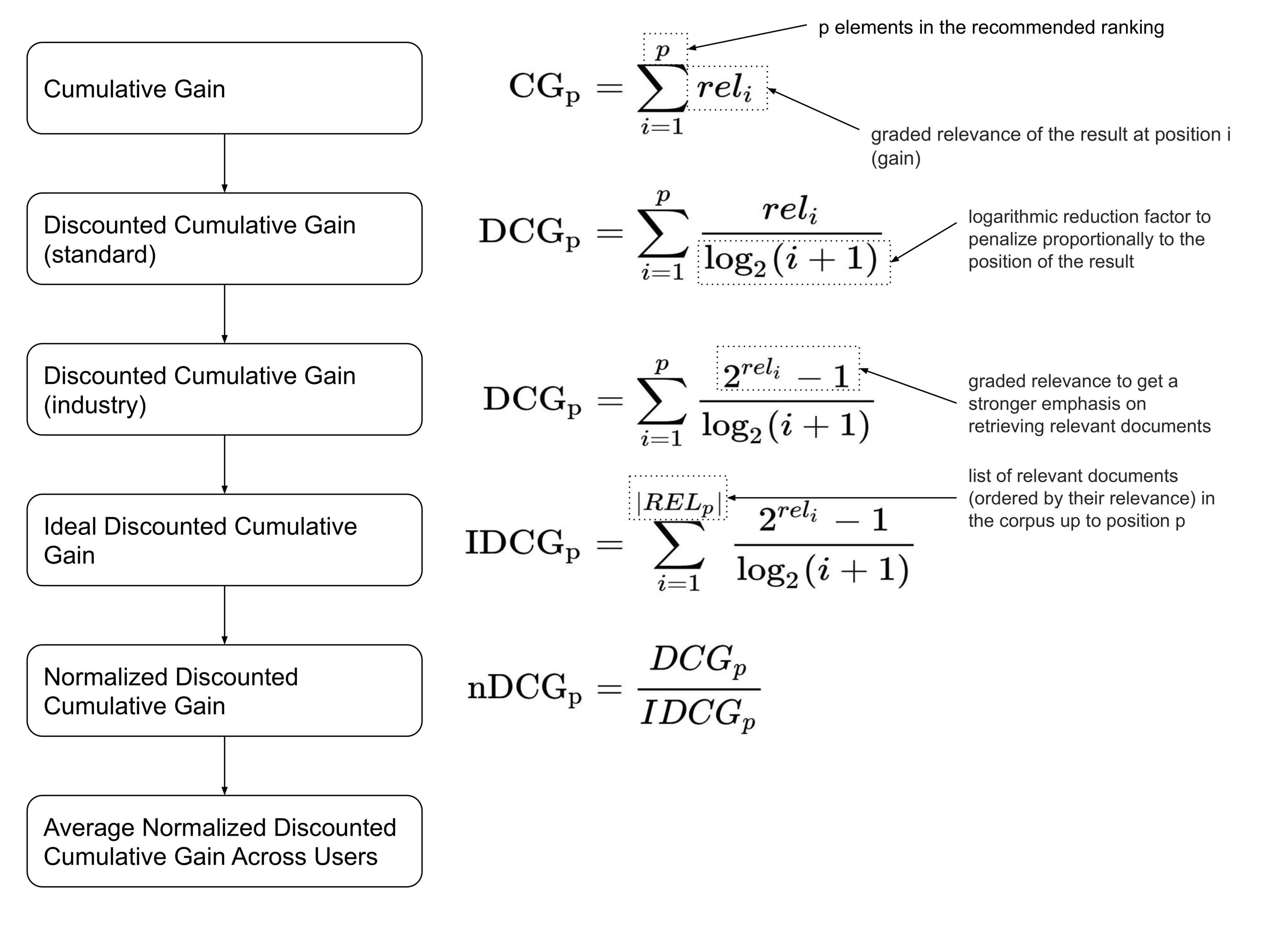
- 모든 추천 컨텐츠들의 관련도를 합하여 CG(cumulative gain)을 구한다.
- CG에서 추천 컨텐츠들의 관련도를 합하였다면, DCG는 각 추천 컨텐츠의 관련도를 log함수로 나누어 값을 구한다. log함수 특성상 위치 값이 클수록(하위에 있을 수록) DCG의 값을 더 작아지게 함으로써 상위 컨텐츠의 값을 점수에 더 반영할 수 있게 한다.
- DCG 값에 관련도를 더 강조하고 싶다면, 2^관련도 - 1과 같이 관련도의 영향을 증가시킬 수 있다.
- 사용자마다 제공되는 추천 컨텐츠의 DCG와는 별개로 IDCG(이상적인 DCG)를 미리 계산해놓는다.
- 각 사용자의 DCG를 IDCG로 나누어서 사용자별 NDCG를 구한다.
- 사용자별 NDCG의 평균을 구하여 해당 IR의 NDCG를 구한다.
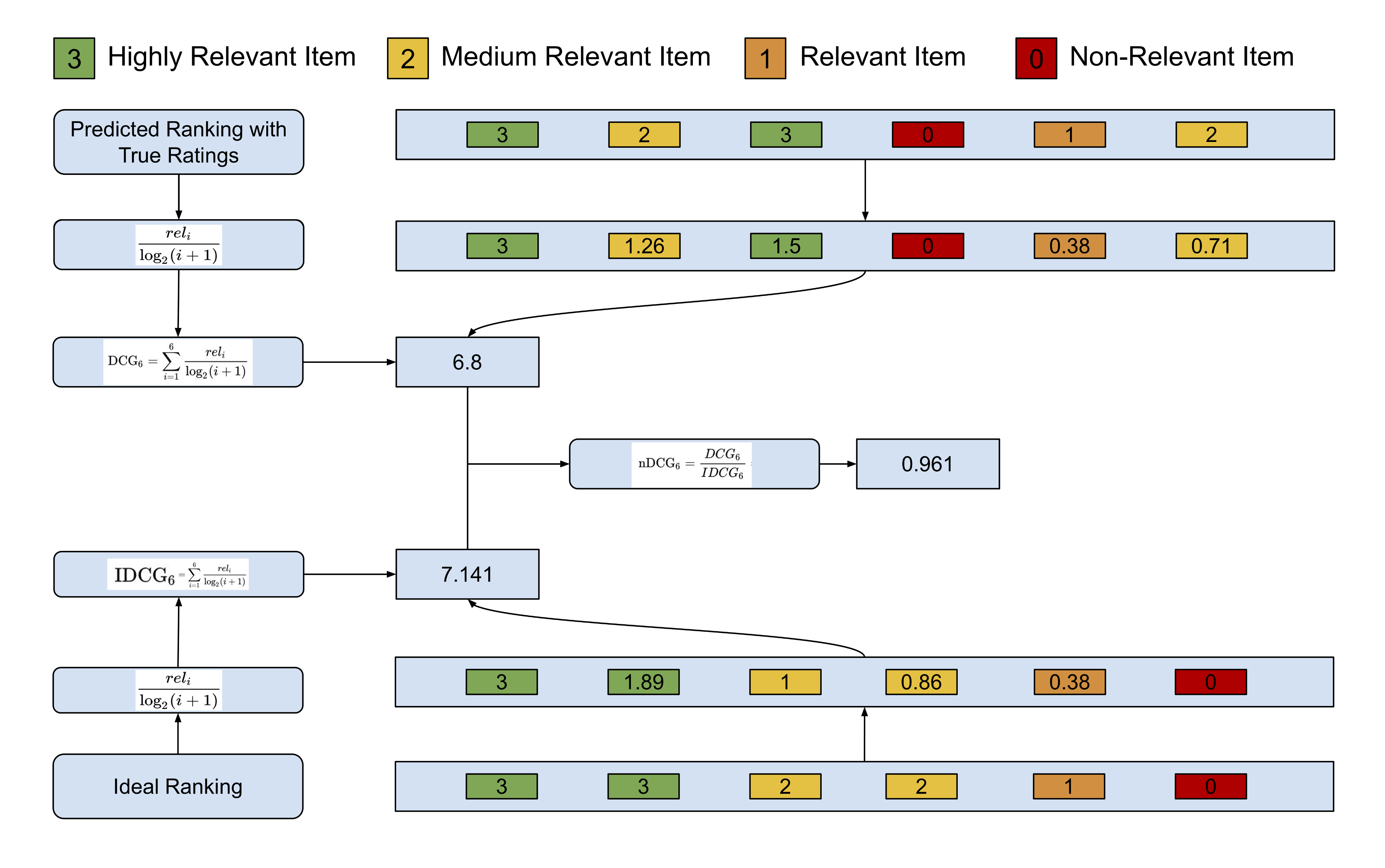
- 맨 밑줄을 보면 정답 랭킹순서가 3,3,2,2,1,0으로 관련 순서대로 점수가 있다.
- 맨 첫줄은 모델이 봤을때 관련도에 대한 점수로 3,2,3,0,1,2로 CG이다.
- 이 둘을 이제 비교하는 것이 NDCG이다.
- 먼저 정답 랭킹순서에 따라, 관련도 높은 문서가 더 가중치가 가도록 log2(i+1)로 나눠준다.
- 예) 2/log(1+2)=1.26이 되는 것
- 이를 순서에 따라 discount을 구한다.
- 예측점수로 구한것 = DCG
- 정답레이블로 구한것 = IDCG
- 최종 score = nDCG = DCG/IDCG
- NDCG 장점
- 기존 방법과는 다르게 다양한 관련도에 대한 평가가 가능하다.
- 이분법적인 관련도에도 뛰어난 성능을 보인다.
- log 함수를 이용하여 하위 컨텐츠에 대한 영향을 줄임으로써 좋은 성능을 보인다.
- NDCG 단점
- 사용자와의 관련성을 파악하기 어려운 상황에는 문제의 소지가 있다.
- 사용자가 컨텐츠에 대한 평가를 하지 않는다면(평점을 입력하지 않는 경우) 해당 관련도를 어떻게 처리해야 할지에 대해 정의해야 한다.
- 0점 처리해도 문제가 될 것이고, 평균 값을 이용해도 문제가 될 수 있다.
- 사용자의 관련 컨텐츠가 없다고 판단될 경우, 임의로 NDCG를 0으로 설정해주어야 한다.
- 보통 K개의 NDCG를 가지고 IR을 평가하는데 IR에서 제공한 컨텐츠가 K보다 부족한 경우, 부족한 관련도를 최소 점수로 채워서 계산해야 한다.





댓글
댓글 쓰기